Cycling enthusiasts often hear terms like Cycling Power and Cycling Torque, yet struggle to grasp them. In this article, we’re breaking down these concepts, making them accessible and easy to understand. With this piece, we promise that you will understand what cycling power and cycling torque are, and how they are calculated.
Invisible Engine Theory
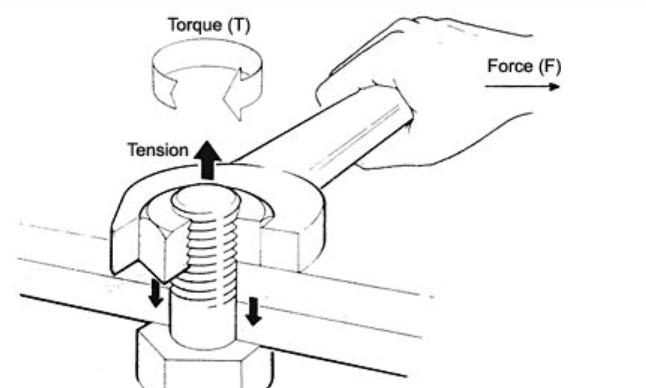
The bike’s power machine is you and your legs. An important criterion for judging how strong your legs are is torque. Torque is instantaneous data. And it is equal to the force you exert on the pedals multiplied by the length of the crank arm. So the unit of cycling torque is Nm. A more powerful athlete can output more instantaneous cycling torque.
As we all know, the feet will exert force on the pedal on both sides, the pedal will drive the crank arm and then the spindle to rotate, and the rotating spindle will drive the chainring to pull the chain. Your legs are the engine of this entire system, used to twist the spindle, making it rotate. But we can’t find a suitable parameter to describe just how powerful your legs are.
So we assume an invisible mechanical engine inside the bottom bracket. This invisible mechanical engine will replace your legs to rotate the spindle, which in turn drives the chainring and chain. As we said, torque is used as a description of how powerful your legs are at a point in time. Similarly, torque can be used to describe how powerful this invisible engine is. If you’re sitting on such a hypothetical bike, the engine runs you and your bike at 30 km/h. Theoretically, your legs will have the same performance, strength and torque as that engine if you can maintain at 30 km/h by exert forces on the pedals.
Straight power and rotational power (cycling power)
The rocket engine outputs linear thrust, if I want to describe how powerful the rocket engine is, I will directly say that this engine thrust is 8000N or can push up 700 tons, which means this engine can provide a upward force that equals the weight of 700 tons, making something weighted 700 tons stay put in the air, or pushing a 500 tons rocket to the outer space while accelerating.
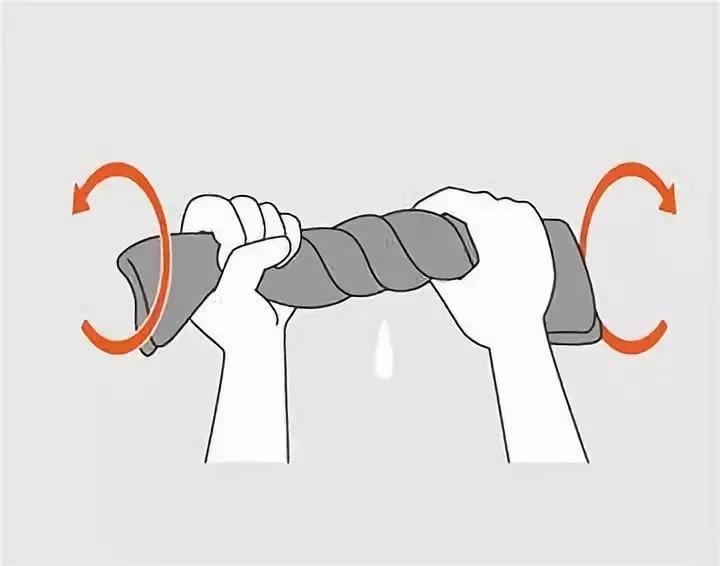
The car engine and the invisible engine we are talking about here do not output linear thrust, but rotating thrust. We of course want to describe how powerful the car engine or this invisible engine is when it twists the spindle. So, the concept of torque was here. You can interpret cycling torque as the force you use to rotate a bike spindle (or crankshaft in a car) with your hand like you twist the throttle handle of a motorcycle or wring the towel.

Cycling Torque = force (N) * force arm (m)
The same rotational force, at different distances from the rotating spindle. Because of the leverage effect, the closer to the axis, the greater the linear thrust. The farther away from the axis, the smaller the linear thrust. But in fact, the rotating force of the invisible engine on the spindle remains the same. The lever theorem tells us that to apply a rotating force of some size, one can apply a larger force near the axis (a small radius) or a smaller force far away from the axis (a large radius). As long as the product of the force and the force arm is the same, the effect is the same.
In turn, for the same rotating force, different positions (radius/force arm) show different force sizes and only the product of force and force arm is always constant. For a rotating force, we cannot describe by a simple parameter how powerful this rotating force is. If I tell you that the rotation force is 10N, how do you know whether it is 10N at the spindle 1mm radius or 10N at the 1km radius from the spindle? Therefore, to measure the rotational force, we can no longer only use Newton (N) as the unit of measurement, but the product of the force and the force arm as the measure, in Nm (Newton * meter). This is the cycling torque.

When you want to apply 30 Nm of cycling torque to the spindle, if you use a 200mm length crank arm, you will have to apply a 150N linear force to the pedal. If you use a 150mm length crank arm, then you have to apply a bigger 200N linear force on the pedal. Your bike gets the same instant in both instances. So in cycling, the cycling torque is equal to the force your foot exerts on the pedal multiplied by the length of the crank arm.
Cycling Power (w) = Torque (Nm) * Rotate speed (rpm)
After understanding the cycling torque above, cycling power becomes easy to understand. If the cycling torque is defined as the strength of the rotational force applied to the spindle, the cycling power is usually defined as the speed of your energy output at some point in time. With equal rotational force on the same spindle, the spindle was twisted at different speeds for 10 minutes. After those 10 minutes, it must be the faster spindle rotation that makes you feel more tired. So, the calculation of cycling power also takes into account the rotation speed of the spindle. In simple terms, the cycling power (w) is equal to the cycling torque (Nm) multiplied by the pivot speed (rpm). It represents your energy output speed. The greater the average power over the same riding time, the more energy you consume.
SUMLON is a bike parts manufacturer and one-stop wholesaler. We manufacture and wholesale several kinds of bike parts, including different size of crank arms. Contact us if you would like to make a discussion about the torque and power mentioned above.